Basic Strategy
- Player I (Spoiler)'s goal is to exploit differences between the graphs to end the game as soon as possible. For instance, suppose the left graph has a vertex which is connected to every other vertex, while the right graph does not.
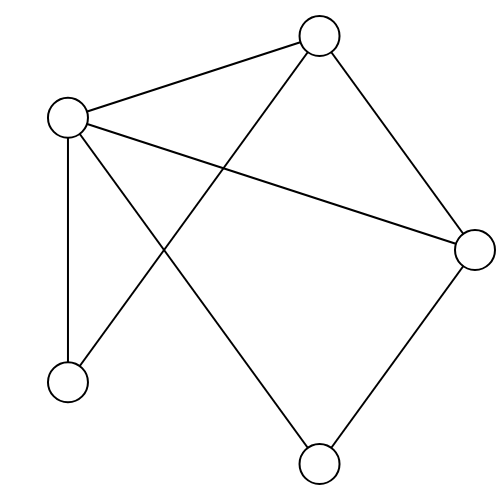
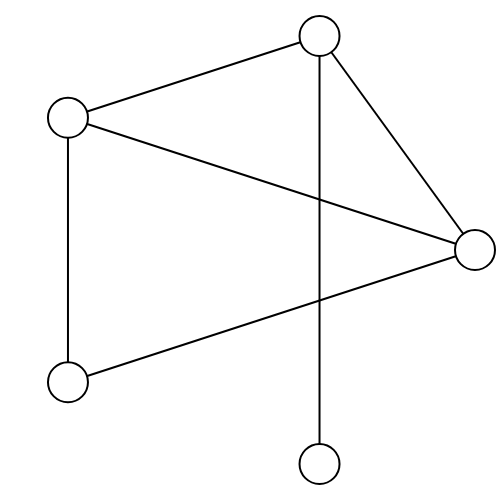
Spoiler can play at the vertex in the left graph which is connected to every other vertex. No matter which vertex Player II (Duplicator) matches it with, that vertex will not be connected to every other vertex.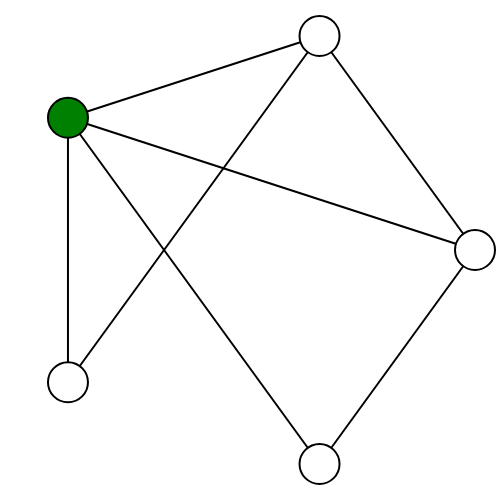
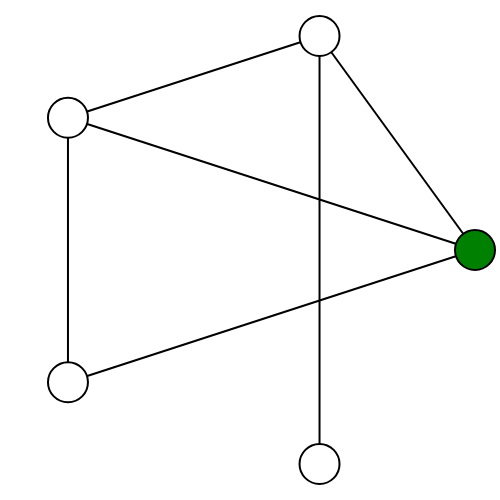
Spoiler can then take advantage of the vertex in the second graph which is not connected to the original vertex to win the game. No matter where Duplicator moves, they have lost.
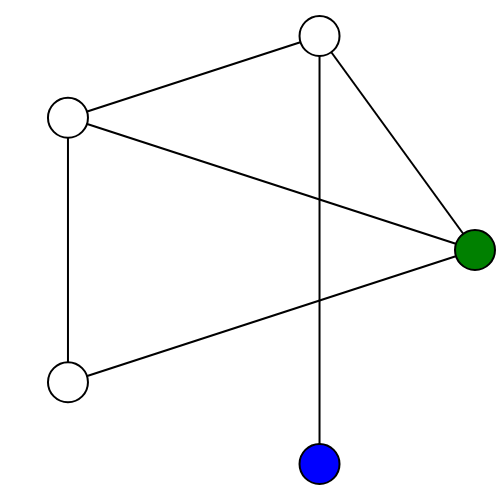
- Player II (Duplicator)'s goal is to exploit similarities between the graphs to prolong the game. In fact, if the two graphs are the same (or scrambled versions of one another), Duplicator can keep the game going as long as possible!
Connection with Logic
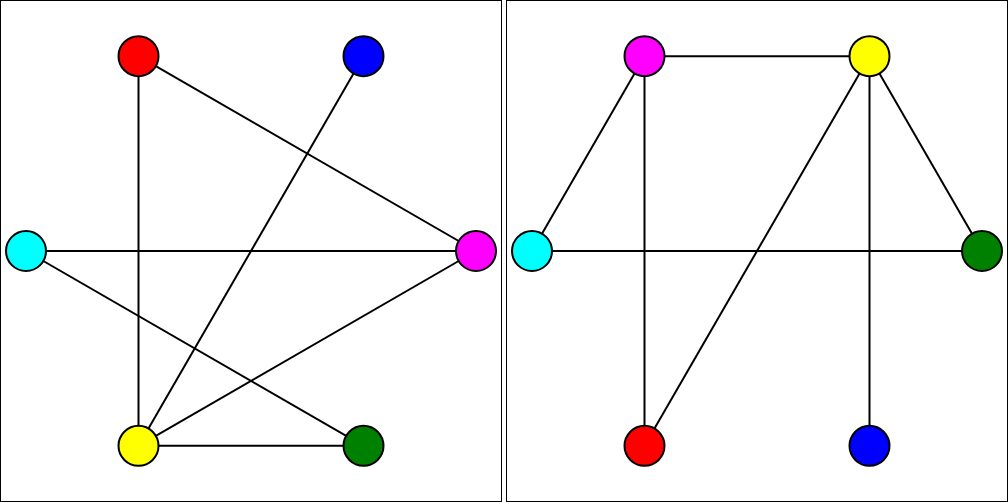
So the main goal of the game is to recognize the similarities and differences between the two graphs. Features to pay attention to include:- If there are no vertices
- If there is a vertex which is connected to every other vertex
- If there is a vertex which is not connected to any other vertex
- If there is a vertex which is connected to every other vertex except one
- If there is a vertex which is not connected to any other vertex except one
- Variables to talk about vertices (a,b,c,etc.)
- There is (another) vertex (∃)
- Every (other) vertex (∀)
- And, Or, Not (∧, ∨, ¬)
- Is connected to (˜)
- Equality and inequality (=/≠)
- Grammatical pieces (such that/it is the case that)
- Is a circle, triangle, square (if shapes are active)
| There is a vertex which is connected to every other vertex | ||||||||
| There is a vertex | a | such that | for every other vertex | b | it is the case that | a | is connected to | b |
| ∃ | a | : | ∀ | b (≠ a) | : | a | ∼ | b |
| ∃ a: ∀ b ≠ a: a ∼ b | ||||||||
Theorem (Ehrenfeucht, Fraïssé): The number of turns it takes for spoiler to exploit a particular difference between two graphs is the minimum number of variables needed to express that difference in the language above.
Furthermore:
- The instructions Spoiler must follow to exploit that difference can be fairly straightforwardly read off of the logical formula expressing that difference.
- The minimum number of turns Spoiler needs to win the game is the number of variables in the formula that distinguishes the two graphs with the fewest variables.
Why do Ehrenfeucht–Fraïssé Games matter?
A major question of logic is what can and what cannot be said in particular formal languages. Think designing a programming language and wanting to make sure that programmers can write programs to do particular things in that language. Ehrenfeucht–Fraïssé Games allow us to take our intuitions about playing games and use them to determine what can and cannot be said in this one particular kind of language.For example consider the following two graphs:
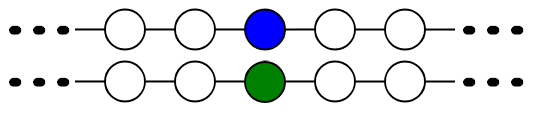
- Left Graph:

A single line of vertices, each connected to the one before it and the one after it, infinite in both directions. - Right Graph:


Two copies of the left graph.
- Variables to talk about vertices (a,b,c,etc.)
- There is (another) vertex (∃)
- Every (other) vertex (∀)
- And, Or, Not (∧, ∨, ¬)
- Is connected to (˜)
- Equality and inequality (=/≠)
- Grammatical pieces (such that/it is the case that)
- Suppose the graphs aren't indistinguishable. Specifically, that there is some logical formula in the above language which is true of one that is false of the other.
- Then that formula has some number of variables (n) in it, and by the Ehrenfeucht–Fraïssé Theorem, Spoiler has a strategy for winning the game in n turns.
- This strategy is going to look something like: On their first two turns, Spoiler plays in both pieces of the right graph:
- Forcing Duplicator to play at two points somewhere (ideally very far apart) on the left graph:
- Spoiler's goal now is to exploit the fact that the selected vertices on the left graph are connected by a (very long) string of vertices whereas they are not connected in such a way on the right graph.
- But, remember that Spoiler claimed not only that they had a winning strategy, but a winning strategy in n turns!
- But, if Duplicator played at two points a certain distance apart (roughly 2n), Spoiler does not have enough time to take advantage of this difference.
- So Spoiler didn't actually have a strategy for winning the game in n turns. (The liar!)
- So the graphs really aren't distinguishable.
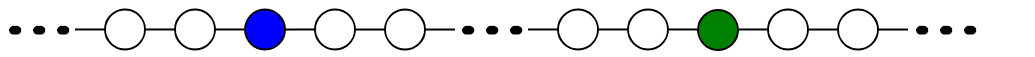
Fun Fact: There is no formula in our particular language that expresses the idea of "being connected" i.e. any two vertices are connected by a string of vertices, each connected to the next.